A. Persamaan Lingkaran yang berpusat di O (0, 0) dan berjari-jari r.

Dari gambar, diperoleh persamaan :
Sehingga diperoleh persamaan lingkaran dengan pusat di O dan berjari-jari r , yaitu :
Suatu titik A
 dikatakan :
dikatakan :
a. Terletak pada lingkaran


b. Terletak di dalam lingkaran
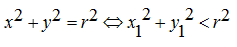
c. Terletak di luar lingkaran
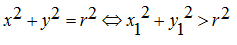
B. Persamaan Lingkaran yang berpusat di P (a, b) dan berjari-jari r.
Gambar di atas adalah sebuah lingkaran dengan pusat (a, b) dan berjari-jari r. Titik Q (x, y) adalah sebuah titik pada lingkaran.
Dari gambar diperoleh persamaan :
Suatu titik A
 dikatakan :
dikatakan :
a. Terletak pada lingkaran

b. Terletak di dalam lingkaran

c. Terletak di luar lingkaran

C. Persamaan Umum Lingkaran
Bila kita menjabarkan persamaan :

Dan mengatur kembali suku-sukunya, maka akan diperoleh :
Persamaan terakhir dapat pula dinyatakan dengan :

Persamaan terakhir dapat pula dinyatakan dengan :

Dengan :


Persamaan (3) merupakan persamaan lingkaran dengan pusat di dan berjari-jari
dan berjari-jari 
D. Persamaan garis singgung lingkaran
1. Garis singgung lingkaran melalui sebuah titik lingkaran
* ditentukan dengan rumus
ditentukan dengan rumus 
* Persamaan garis singgung melaui titik P pada lingkaran
pada lingkaran 
dinyatakan dengan rumus :

Maka persamaan garis singgungnya :
3. Garis singgung melalui sebuah titik diluar lingkaran
Dari suatu titik P yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.
yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.
 terletak di luar garis lingkaran adalah :
terletak di luar garis lingkaran adalah : 
Langkah menentukan gradien ( m ) untuk persamaan (10) adalah sebagai berikut :
1. Substitusikan persamaan ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.
ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.
2. Dengan mengambil nilai D=0 , maka dipetoleh nilai m.


Persamaan (3) merupakan persamaan lingkaran dengan pusat di
 dan berjari-jari
dan berjari-jari 
D. Persamaan garis singgung lingkaran
1. Garis singgung lingkaran melalui sebuah titik lingkaran
*
 ditentukan dengan rumus
ditentukan dengan rumus 
* Persamaan garis singgung melaui titik P
 pada lingkaran
pada lingkaran 
dinyatakan dengan rumus :

*Persamaan garis singgung melaui titik P pada lingkaran
pada lingkaran 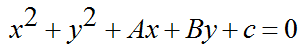 dinyatakan dengan rumus :
dinyatakan dengan rumus : 
2. Garis singgung dengan gradien yang diketahui.
* Jika garis y = mx + n menyinggung lingkaran  pada lingkaran
pada lingkaran 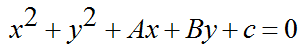 dinyatakan dengan rumus :
dinyatakan dengan rumus : 
2. Garis singgung dengan gradien yang diketahui.

Maka persamaan garis singgungnya :

3. Garis singgung melalui sebuah titik diluar lingkaran
Dari suatu titik P
 yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.
yang terletak di luar garis lingkaran dapat dibentuk dua garis singgung.
 terletak di luar garis lingkaran adalah :
terletak di luar garis lingkaran adalah : 
Langkah menentukan gradien ( m ) untuk persamaan (10) adalah sebagai berikut :
1. Substitusikan persamaan
 ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.
ke persamaan lingkaran sehingga diperoleh suatu persamaan kuadrat.
2. Dengan mengambil nilai D=0 , maka dipetoleh nilai m.







tolong di beri contoh soalnya juga dan cara mengerjakan, agar nanti lebih paham
BalasHapusterima kasih
penjelasannya rumus doang. terlalu singkat. logikanya tidak jelas. saya sangat menentang aliran matematika yang seperti ini karena telah menyesatkan saya selama bertahun2. go to hell.
BalasHapusaku juga buat... ada contoh soalnya lho... :)
BalasHapushttp://mediabelajaronline.blogspot.com/2011/10/persamaan-lingkaran.html
asal rumusnya ngaco -___-". jd makin gk ngerti
BalasHapuspengaturan rumus nya bagus, jd mudah utk dipelajari, cuma... rumusnya ada bbrp yg salah dan penggunaan notasi C dan c sebaiknya diperbaiki karena bisa menyesatkan.
BalasHapusrumus nya lengkap dan jelas sekali..
BalasHapusterimakasih banyak atas bantuan nya!
sangat menolong saya utk persiapan ujian semester!
penjelasan.y kaya taiiiiiiiiiiiiiii
BalasHapusThx penjelasannya
BalasHapusBnyak yg kurang n ngaco,.
BalasHapusrumusnya aneh.
BalasHapusKomenya lucu2. . Bhahahahahahaha. . . . .
BalasHapusmau belajar jd malah bingung.. materi saya jg sampe sini -_-'?
BalasHapusjadi bingung T.T
BalasHapusbanyak rumusnya yang salah oooommmm
BalasHapusiya nih banyak yg salah, update lg dong
BalasHapuslol for u all
BalasHapusGood. Thanks yes :)
BalasHapusKalau melalui tiga titik, misalnya (5,3) , (6,2) , (3, -1) ?
BalasHapusBundel lingkaran itu gimana ya ?
BalasHapusKalo paham materi rumus ini bisa digunakan krn rangkuman
BalasHapus