SUKU BANYAK

A. Suku Banyak (Polinom)

Bentuk Umum :
dimana : 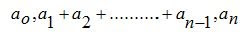adalah konstanta , n bilangan cacah.
Pangkat tertinggi x menyatakan derajat suku banyak.
Contoh :

B. Menghitung Suku Banyak/Nilai Suku Banyak

Misal :

Cara Menghitung :
1. Dengan Substitusi
Jika , maka nilai suku banyak tersebut x = -1 atau f (-1) .


2. Dengan pembagian sistem horner
Jika adalah suku banyak, maka f (h) diperoleh dengan cara berikut :

C. Pembagian Suku Banyak

Secara matematis dapat ditulis :

* Jika pembaginya fungsi linier, maka hasil bagi dan sisanya dapat dicari dengan cara metode pembagian sintetis Horner
* Jika pembaginya bukan linier dan tidak dapat diuraikan maka digunakan metode identitas.

Contoh:
Tentukan hasil bagi dan sisa pembagian suku banyak: dengan x -1 dengan menggunakan metode sintesis Horner!
Jawab :
Pembagian adalah (x-1), berarti k = 1
Kita gunakan metode sintetik berikut:

Dari bagan diatas terlihat bahwa hasil bagi adalah (x-1) dan sisa 40

D. Teorema Sisa

1. Suatu suku banyak f ( x ) jika dibagi ( x – a ) maka sisanya = f ( a )

2. Suatu suku banyak f( x ) jika dibagi ( x + a) maka sisanya f (-a)

3. Suatu suku banyak f ( x ) jika dibagi (ax – b) maka sisanya =

4. Suatu suku banyak f ( x ) habis dibagi (x – a) maka f (a) = 0

E. Teorema Faktor

1. Jika pada suku banyak f (x) berlaku f (a) = 0 dan f (b) = 0 maka f (c) = 0 maka f (x) habis dibagi

(x – a)(x – b)(x – c).

2. Jika (x – a) adalah faktor dari f (x) maka x = a adalah akar dari f (x).

3. Jika f (x) dibagi oleh (x – a)(x – b) maka sisanya :

4. Jika f (x) dibagi oleh (x – a)(x – b)(x – c) maka sisanya :