EKSPONEN

1. Pengertian Eksponen
Bentuk aⁿ (baca : a pangkat n) disebut bentuk eksponensial atau perpangkatan dengan a disebut basis atau bilangan pokok dan n disebut eksponen atau pangkat.
Jika n adalah bilangan bulat positif, maka :

Berdasarkan penjelasan di atas maka berlaku rumus-rumus di bawah ini :
Misalkan dan m,n adalah bilangan positif, maka:




Contoh:
Ubahlah bentuk ini dalam bentuk pangkat positif :
Jawab:



2. Fungsi Eksponen dan Grafiknya
Fungsi eksponen merupakan pemetaan bilangan real x ke a^x dengan a > 0 dan Jika a > 0 dan , maka disebut fungsi eksponen mempunyai sifat-sifat :

(i) Kurva terletak di atas sumbu x (definit positif)

(ii) Mempunyai asimtot datar y = 0 (sumbu x )

(iii) Monoton naik untuk a > 1

(iv) Monoton turun untuk 0 <>

Grafik fungsi eksponen y = a^x

(i) y = a^x : a > 1

(i) y = a^x 0 <>

Contoh:
Buatlah grafik dari y = 2^x!
Jawab:
Buatlah tabel yang menunjukkan hubungan antara x dan y = f (x) = 2^x . Dalam hal ini pilih nilai x sehingga y mudah ditentukan.



3. Persamaan fungsi Eksponen
Ada beberapa bentuk persamaan eksponen, diantaranya adalah:

- F ( x ) = 1

- Untuk f(x) 0 dan f(x) 1, maka f(x) = g(x)

- f ( x ) = -1 asalkan f (x) dan g (x) sama-sama genap atau sama-sama ganjil,

- f ( x ) = 0 asalkan f ( x ) > 0 dan g ( x ) > 0

Contoh :
Tentukan nilai x supaya
Jawab:

4. Pertidaksamaan Eksponen

1. f ( x ) > g ( x ), 0 > 1

2. f ( x ) <>

Contoh:

Himpunan bilangan real yang memenuhi pertidaksamaan adalah....
Jawab:

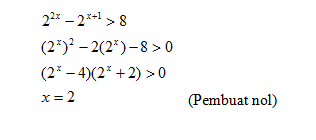
Jadi HP = { x | x > 2 }