Transformasi T dibidang adalah suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama.
Jenis-jenis transformasi yang dapat dilakukan antara lain :
- Translasi (Pergeseran)
- Refleksi (Pencerminan)
- Rotasi (Perputaran)
- Dilatasi (Perkalian)
2. Translasi dan Operasinya
Translasi (pergeseran) adalah pemindahan suatu objek sepanjang garis lurus dengan arah dan jarak tertentu.
Jika translasi
 memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
Contoh : Tentukan koordinat bayangan titik A (-3, 4) oleh translasi

Jawab :
Jawab :
A’ = ( -3 + 3, 4 + 6)
A’ = (0, 10)
3. Refleksi (Pencerminan)
a. Pencerminan terhadap sumbu x
Matriks percerminan :
b. Pencerminan Terhadap sumbu y
Matriks Pencerminan:
c. Pencerminan terhadap garis y = x
d. Pencerminan terhadap garis y = -x
Matriks Pencerminan:
e. Pencerminan terhadap garis x = h
Sehingga:
f. Pencerminan terhadap garis y=k
Sehingga:
g. Pencerminan terhadap titik asal O (0, 0)
Sehingga:
h. Pencerminan terhadap garis y = mx dimana m = tan q
Contoh :
Tentukan bayangan persamaan garis y = 2x – 5 oleh translasi 
Jawab :
Ambil sembarang titik pada garis y = 2x – 5, misalnya (x, y) dan titik bayangan oleh translasi 
Atau
x’ = x + 3 
y’ = y – 2 
Persamaan (1) dan (2) disubtitusikan pada persamaan garis semula, sehingga :
y = 2x – 5
y’ + 2 = 2 (x’- 3) – 5
y’ = 2x’ – 6 – 5 – 2
y’ = 2x’ – 13
Jadi persamaan garis bayangan y = 2x – 5 oleh translasi 
REFERENSI:
lks MATEMATIKA SMU KELAS XII











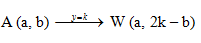
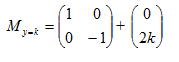






Makasiiii :)
BalasHapusbaguuuuuuuuuuus......
BalasHapusmatur suwund sanget....
BalasHapusbagus....
BalasHapussoal2 laine mana bos
mank ga' da soal laen ya?????????????????
BalasHapusHatur nuhun,,
BalasHapusMakasih Gan, materi.a sgtmmbntu. Lg di sruh bkin rangkuman rumus nih. Makasih ya Gan !
BalasHapusUpdate trus Blog.a ya !
dikasih contoh dong refleksi terhadap garis y = mx + c; truz yang bener y - n atau y - m
BalasHapusTentukan bayangan titik (-3,7) terhadap garis 2x-y+3=0.
HapusPenyelesaian:
tan x = 2, maka sin x = 2/V5, cos x = 1/V5.
Dengan menggunakan rumus (h), diperoleh matriks [-3/5 4/5;4/5 3/5][-3;7-3]+[0;3]=[-3/5 4/5;4/5 3/5][-3;4]+[0;3]=
[5;3]. Sehingga diperoleh bayangannya (5,3).
Notes: untuk matriks transformasi
[cos 2x sin 2x;sin 2x -cos 2x]=
[1-2sin^2(x) 2sinxcosx; 2sinxcosx -(1-2sin^2(x))]
matur nuwun om, berguna sanget kagem tugas kulo
BalasHapusterimakasih banyak :)
BalasHapusbelajar matematika memang asyik.,
BalasHapusasyik my ass
Hapusartikel yang bermanfaat, kalau bisa dikasih soalny juga mas...slam kenal . . .
BalasHapusMakasih atas postiganx ini . . .
BalasHapusini sangant 3x membantu . . .
terimakasih sebelunya, tapi kenapa penjelasan rotasi dan dilatasinya tidak ada?
BalasHapusmasak sih ini pelajaran SMA disekolahku ini sdh dipelajari...!!!
BalasHapusAku baru kelas 7
sejak kapan kelas 7 udah termasuk SMA? yg ada kelas 7 itu masih SMP kalii
Hapusni kan pelajaran kelas 6????????????
BalasHapusmakasihh..Braaayyyy.....
BalasHapuska, kalau mencari gradien bila yang diketahui P(2,-3) dan P'(4,5)... caranya gimana ya? itu refleksi terhadap y=mx+c.
BalasHapusmakasi ya bermanfaat bgt
BalasHapusKalo rumus tentukan hasil translasi titik A (1,3) dan B (-2,1) oleh T=[1 dibawah 3].
BalasHapusmksih
BalasHapusterima kasih atas info yang anda berikan.. sangat bermanfaat :)
BalasHapusmakasih contekannya sayy
BalasHapusmana rotasi sama dilatasinya? saya butuh nih
BalasHapusWater flows from a high place to a lower place. If the water that fell from a height
BalasHapustogel online
Berguna, makasi
BalasHapusterimakasih bnyak atas materinya,
BalasHapusdan saya berharap materiny lebih banyakdan mudah dimengerti ^^
very helpfull
BalasHapus