Notasi sigma adalah sebuah tanda yang digunakan untuk menuliskan penjumlahan secara singkat. Notasi sigma, ditulis dengan

Secara umum, notasi sigma didefinisikan sebagai berikut :

Dimana:
i adalah indeks penjumlahan
n adalah batas bawah penjumlahan
n adalah batas atas penjumlahan
Sifat-sifat notasi sigma:





Contoh :
Tentukan

Jawab:

2. Barisan dan Deret Aritmatika
Suatu barisan
 disebut barisan aritmatika jika selisih antara dua suku yang berurutan selalu tetap, selisih tersebut dinamakan beda yang dilambangkan dengan “b”.
disebut barisan aritmatika jika selisih antara dua suku yang berurutan selalu tetap, selisih tersebut dinamakan beda yang dilambangkan dengan “b”.
Jika suku pertama dinyatakan dengan a, maka bentuk umum barisan aritmatika adalah :

Apabila a menyatakan suku pertama, n menyatakan banyak suku dan b menyatakan beda, maka :
1. Suku ke – n barisan aritmatika (Un) dirumuskan sebagai :

2. Jumlah n suku pertama deret aritmatika (Sn) dirumuskan sebagai:
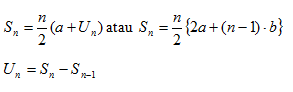
3. Untuk n ganjil, maka suku tengah barisan aritmatika (Ut) dirumuskan sebagai:

4. Sisipan dalam deret aritmatika

dimana : b = beda sebelum di sisipi, b'= beda yang baru setelah disisipi
5. Banyaknya suku baru setelah disisipi (n')

6. Jumlah n suku pertama sesudah sisipan

Contoh:
1. Diketahui barisan aritmatika 5, 8, 11, ...., 125, 128, 131. Suku tengahnya adalah .....
Jawab:
Barisan aritmatika : 5, 8, 11, ……, 131
a = 1 , Un = 131
suku tengah :

2. Jumlah n buah suku pertama suatu deret aritmatika dinyatakan oleh
 Beda deret tersebut adalah:
Beda deret tersebut adalah:
Jawab:


3. Berapakah jumlah semua bilangan-bilangan bulat diantara 100 dan 300 yang habis dibagi oleh 5?
Jawab:
Barisan diantara 100 dan 300 yang habis dibagi 5 ;
105, 110, 115, ....., 295
a = 105, b = 5 dan Un = 29
Un = a + (n – 1) . b
295 = 105 + (n – 1) . 5
190 = 5n – 5
5n = 195
n = 39
3. Barisan dan Deret Geometri
Suatu barisan geometri jika perbandingan antara dua suku yang berurutan ( r ) selalu tetap.

Rasio yang baru setelah deret geometri disisipi k bilangan adalah :

Untuk n ganjil, suku tengah barisan geometri :

Contoh:
1. Diketahui barisan geometri 1, 2, 4, 8, ...... Bila jumlah n suku pertama, adalah 2047, berapakah Ut ?
Jawab :
1, 2, 4, 8, ......
a = 1, r = 2 , Sn = 2047
Karena r > 1, maka :
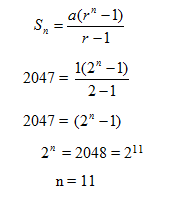

2. Suku kelima dan suku kedelapan suatu barisan geometri berturut-turut adalah 48 dan 384. Suku keempat barisan tersebut adalah ....
Jawab:


Maka:

4. Deret Geometri Tak berhingga
Pada deret geometri, untuk  maka deret tersebut dikatakan deret geometri tak berhingga. Bentuk umum deret geometri tak berhingga adalah sebagai berikut :
maka deret tersebut dikatakan deret geometri tak berhingga. Bentuk umum deret geometri tak berhingga adalah sebagai berikut :
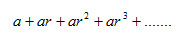
Deret geometri tak berhingga dikatakan konvergen (mempunyai limit jumlah) jika -1 <>
Jika maka deret tersebut dikatakan divergen (tidak mempunyai limit jumlah,sehingga :
maka deret tersebut dikatakan divergen (tidak mempunyai limit jumlah,sehingga :

Contoh:
suku ke n deret geometri adalah 4-n maka jumlah tak berhingga deret tersebut adalah:


 maka deret tersebut dikatakan deret geometri tak berhingga. Bentuk umum deret geometri tak berhingga adalah sebagai berikut :
maka deret tersebut dikatakan deret geometri tak berhingga. Bentuk umum deret geometri tak berhingga adalah sebagai berikut :
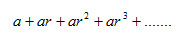
Deret geometri tak berhingga dikatakan konvergen (mempunyai limit jumlah) jika -1 <>

Jika
 maka deret tersebut dikatakan divergen (tidak mempunyai limit jumlah,sehingga :
maka deret tersebut dikatakan divergen (tidak mempunyai limit jumlah,sehingga :

Contoh:
suku ke n deret geometri adalah 4-n maka jumlah tak berhingga deret tersebut adalah:



mkasih yow notasi sigma_ny...
BalasHapusjalan keluar bwt aq...
thx ya, gw jd ngerti :D
BalasHapusdapet rumus suku tengah dari mana yah?
BalasHapusThank atas infox
BalasHapusthankz,,,,,,,,dg info nhe gw sa gkutin kulyah dg baek,,,,,,
BalasHapus3+5+9+15
BalasHapusrumus gigmanya berapa
3+5+9+15.....
BalasHapusrumus sigmanya berapa ya????
artikelnya bgus,,, maw nanya untuk sigma n btas atas yg mana n bts bwah yg mn..
BalasHapussiiip
BalasHapusmana???
BalasHapusmasih bingugn, kalo notasi sigma itu pengertian awalnya gmn?
notasi sigma bisa di sebut begini ga?
Notasi sigma adalah deret baris arit matika...? ya ga mas...!!!
trima kasih sangat membantu infonya
BalasHapusmau tanya rumus sigma Y pangkat 2 berapa ya jika Y=136
BalasHapusthanks info nya
BalasHapusthanks atas infonya
BalasHapussoalnya tentang notasi sigma tolong diperbanyak ya....?
mantab gan infonya .. sukses selalu
BalasHapusOke banget gan...
BalasHapusThanks gan udah bagi ilmunya...
Terimakasih ya.. atas rumus notasi sigma nya..
BalasHapusterimakasih. sngat membentu di tingkat dasar. tapi mulai pusing lagi kalo udah masuk ke transformasi z :D
BalasHapusMantap do ba, alai lilu au dibaen..
BalasHapuskeren tapi gimana kalo sigmanya memiliki jarak yang panjang antara batas bawah dan batas atasnya?
BalasHapuskeren tapi gimana kalo sigmanya memiliki jarak yang panjang antara batas bawah dan batas atasnya?
BalasHapusGan minta pembuktian sifat sigma no 8 dong . penting nih
BalasHapuskalo rumus Sn untuk aritmatika bertingkat ada g?
BalasHapusbanyak informasi yang saya dapat dari blogg ini sukses terus buat admin bloggnya.. Terus berkarya dan update artikel terbaru lebih banyak lagi ^_^
BalasHapusIni rumus sigma intinya gimana?maaf yg tau tolong balas. Misal sigma 34 itu brp dan agaimana cara dptinnya
BalasHapusIni rumus sigma intinya gimana?maaf yg tau tolong balas. Misal sigma 34 itu brp dan agaimana cara dptinnya
BalasHapusMaaf ya kk mau tanya kenapa sigma atas sama bawah itu dikurang?padahal ga ada batas atas atau bawahnya
BalasHapus